Este projeto foi desenvolvido a partir de meu último tutorial: “Rex”, um robô que nunca perde a linha! Depois de se conseguir desenvolver um robô com capacidade para seguir linhas, o próximo passo natural é sem dúvida, dar-lhe algum grau de inteligência. Assim, nessa etapa, o nosso querido “Rex, o Robô” tentará encontrar uma forma de escapar de um “labirinto” tomando o caminho mais curto e o mais rápido possível.
A propósito, Rex odeia o Minotauro….. 😉
A maioria dos labirintos, por mais complexa sua concepção possa parecer, foram essencialmente formados a partir de uma parede contínua com muitos cruzamentos e bifurcações. Se a parede circundante do objectivo final de um labirinto está ligado ao perímetro do labirinto na entrada, o labirinto sempre poderá ser resolvido mantendo-se uma mão em contacto com a parede, não importando os muitos desvios que possam existir. Estes labirintos “simples” são conhecido como “Simply-connected” ou “perfeitos”, ou em outras palavras, que não contêm loops.
Voltando ao nosso projeto, ele será dividido em duas partes:
- (Primeira passada): O robô encontrará o seu caminho para sair de um labirinto perfeito desconhecido. Não importa onde você o colocar dentro do labirinto, ele sempre encontrará uma “solução de saída”.
-
(Segunda passada): Uma vez que o robô encontrou uma possível solução para sair do labirinto, ele deve otimizar-la, encontrando o caminho mais curto para ir do início ao fim.
O vídeo abaixo, mostra um exemplo do robô encontrando seu caminho para sair do labirinto (chegar “ao final”). Na primeira vez que o robô explora o labirinto, é claro que vai perder muito tempo “pensando” sobre o que fazer em todo e qualquer cruzamento. Para testar as possibilidades, ele tomará vários caminhos errados e becos sem saída, o que faz com que ele escolha caminhos mais longos e execute várias “marcha-rés” desnecessárias.
Durante esta”1ª passada”, o robô irá acumulando experiências, “tomando notas” sobre os diferentes cruzamentos e eliminando os atalhos ruins. Em sua “segunda passada”, o robô irá direta e rapidamente ao final do labirinto sem qualquer erro ou dúvida. Ao longo deste tutorial, exploraremos em detalhes como fazê-lo:
LISTA DE MATERIAIS:
A lista de materiais é basicamente a mesmo que usamos com robô seguidor de linha, exceto que foram incluídos 2 Sensores adicionais para uma melhor precisão na detecção da cruzamentos a esquerda e a direita. O preço final do robô, continua barato (cerca de US$85,00):
- Corpo (pode ser adaptado para as suas necessidades):
- 2 quadrados de madeira (80x80mm)
- 3 Grampos de papel
- 2 rodas de madeira (diâmetro: 50 mm)
- 1 roda “solta” (Caster)
- 9 Elásticos
- Fita 3M “Command”
- Articulações plásticas para fixação do sensor
- Protoboard e fiação
- 2 conjuntos de baterias (4XNi-metal hidreto) – 5V cada conjunto
- 2 Servos de Rotação Contínua (SM-S4303R)
- Arduino Nano
- Módulo Bluetooth HC-06
- 5 sensores x Linha (TCRT5000 4CH Infrared Linha Pista Seguidor Módulo Sensor + 1 sensor de Pista independente)
- 2 sensores ZX03 (baseado no TCRT5000) Reflective Infrared Sensors (saída analógica)
- 1 LED
- 1 Botão
ALTERAÇÕES AO CORPO DO ROBÔ
Retirar o conjunto original dos 5 Sensores e fixar os novos sensores reflectivos aos extremos esquerdo e direito da barra de suporte plástica.
É aconselhável manter os 7 sensores o mais alinhado possível.
Instalação e testes dos novos sensores
A nova matriz de 7 sensores, é montado de forma a que os 5 originais sejam utilizados exclusivamente para o controlo PID e detecção da “linha completa” (explicado mais adiante) e que os novos 2 sensores somente para a detecção dos cruzamentos a esquerda e a direita.
Como uma rápida revisão, vamos lembrar como os 5 sensores originais “digitais” trabalham:
Se um sensor está centrado em relação à linha preta, este irá produzir um sinal HIGH. Por outro lado, o espaço entre os sensores devem ser calculados de tal modo a permitir que dois sensores possam cobrir a largura total da linha preta produzindo assim um sinal HIGH simultaneamente em ambos os sensores.
Como os 2 novos sensores “analógicos” trabalham:
Se um dos sensores está centrado em relação à linha preta, o resultado observado na saída do ADC interno do Arduino será geralmente menor que “100” (lembre-se que o ADC produz uma saída que vai de 0 a 1023). Sobre superfícies mais claras, o valor de saída deverá ser maior (500 a 600 sobre papel branco, por exemplo). Estes valores devem ser testado em diferentes situações de luz de superfície e de materiais para se definir a constante LIMIAR (“THRESHOLD”) correta a ser usada (ver o quadro aqui).
Abaixo, o diagrama mostrando os componentes conectados ao Arduino:

Olhando o código do Arduino, cada um dos sensores será definido com um nome específico:
// LFSensor more to the Left is "0" const int lineFollowSensor0 = 12; //Using Digital input const int lineFollowSensor1 = 18; //Using Analog Pin A4 as Digital input const int lineFollowSensor2 = 17; //Using Analog Pin A3 as Digital input const int lineFollowSensor3 = 16; //Using Analog Pin A2 as Digital input const int lineFollowSensor4 = 19; //Using Analog Pin A5 as Digital input const int farRightSensorPin = 0; //Analog Pin A0 const int farLeftSensorPin = 1; //Analog Pin A1
Recordando, as possíveis combinações de saída para a matriz de 5 sensores original do seguidor de linha são:
- 0 0 0 0 1
- 0 0 0 1 1
- 0 0 0 1 0
- 0 0 1 1 0
- 0 0 1 0 0
- 0 1 1 0 0
- 0 1 0 0 0
- 1 1 0 0 0
- 1 0 0 0 0
Com a adição dos 2 novos sensores, as suas saídas possíveis são:
- Sensor Esquerdo: Saída Analógica maior ou menor do que o valor definido de THRESHOLD
- Sensor Direito: Saída Analógica maior ou menor do queo valor definido de THRESHOLD
A fim de armazenar os valores de cada um dos sensores uma variável tipo matriz (Array) é criada para os sensores digitais originais 5:
int LFSensor[5]={0, 0, 0, 0, 0};
E duas variáveis do tipo inteiras para os 2 novos sensores analógicos:
int farRightSensor = 0; int farLeftSensor = 0;
As variáveis serão constantemente actualizadas dependendo do estado de cada um dos sensores:
LFSensor[0] = digitalRead(lineFollowSensor0); LFSensor[1] = digitalRead(lineFollowSensor1); LFSensor[2] = digitalRead(lineFollowSensor2); LFSensor[3] = digitalRead(lineFollowSensor3); LFSensor[4] = digitalRead(lineFollowSensor4); farRightSensor = analogRead(farRightSensorPin); farLeftSensor = analogRead(farLeftSensorPin);
Possuindo 5 sensores, como se viu no projeto do Robô seguidor de linha, se permite a geração de uma “variável de erro” que ajudará a controlar a posição do robô sobre a linha. Essa variável de erro será mantida e uma nova denominada “mode” será incluída para saber se o robô está seguindo uma linha, sobre uma linha contínua, uma intersecção ou fora da linha.
Esta variável “mode” será usada também com os novos sensores de esquerda e direita. Consideremos que os novos sensores da esquerda e da direita geraram 3 estados possíveis: H (maior do que THRESHOLD), L (menor do que oTHRESHOLD) e X (irrelevante). Para as saídas digitais, manteremos “0”, “1” e também introduziremos o “X”:

X 1 1 1 1 1 X ==> mode = CONT_LINE; error = 0;
H 0 X X X X L ==> mode = RIGHT_TURN; error = 0; (Veja o exemplo na imagem acima)
L X X X X 0 H ==> mode = LEFT_TURN; error = 0;
X 0 0 0 0 0 X ==> mode = NO_LINE; error = 0;
H 0 0 0 0 1 H ==> mode = FOLLOWING_LINE; error = 4;
H 0 0 0 1 1 H ==> mode = FOLLOWING_LINE; error = 3;
H 0 0 0 1 0 H ==> mode = FOLLOWING_LINE; error = 2;
H 0 0 1 1 0 H ==> mode = FOLLOWING_LINE; error = 1;
H 0 0 1 0 0 H ==> mode = FOLLOWING_LINE; error = 0;
H 0 1 1 0 0 H ==> mode = FOLLOWING_LINE; error = -1;
H 0 1 0 0 0 H ==> mode = FOLLOWING_LINE; error = -2
H 1 1 0 0 0 H ==> mode = FOLLOWING_LINE; error = -3;
H 1 0 0 0 0 H ==> mode = FOLLOWING_LINE; error = -4;
Assim, a implementação da lógica acima na função:
void readLFSsensors()
irá retornar as variáveis “mode” e “error” que serão utilizados na lógica do programa.
É importante testar a lógica dos sensores antes de seguir com o projeto. A função de teste abaixo está incluída no código e poderá ser usado para fins de ensaio:
void testSensorLogic(void)
{
Serial.print (farLeftSensor);
Serial.print (" <== LEFT RIGH==> ");
Serial.print (farRightSensor);
Serial.print (" mode: ");
Serial.print (mode);
Serial.print (" error:");
Serial.println (error);
}
Resolvendo o labirinto – a regra da mão esquerda
Como discutido na introdução deste tutorial, a maioria dos labirintos são essencialmente formados a partir de uma parede contínua com muitos cruzamentos e desvios.
Pesquisando na Wikipedia, aprendemos que “o seguidor da parede” é o algorítmo mais conhecido para percorrer labirintos. É também conhecido como “regra da mão esquerda” ou a “regra da mão direita”. Se o labirinto é simplesmente conectado, isto é, todos as suas paredes são ligadas entre si, mantendo-se uma mão em contato com uma das paredes do labirinto é garantido que chegará a uma saída. Usaremos aqui a “Regra da mão esquerda”.
Em resumo, a regra da mão esquerda pode ser descrito como:
- Coloque a mão esquerda na parede.
- Comece a andar para a frente
- Em cada cruzamento, e ao longo do labirinto, manter a sua mão esquerda tocando na parede à sua esquerda.
- Eventualmente, você vai chegar ao final do labirinto. Você provavelmente não vai seguir o caminho mais curto e mais direto, mas você chegará lá.
Portanto, a chave aqui é identificar as intersecções, definindo que medidas tomar com base nas regras acima. Especificamente no nosso tipo de labirinto em 2D , podemos encontrar 8 tipos diferentes de intersecções :

Olhando a imagem acima, podemos perceber que as possíveis ações nos cruzamentos são:
- Em um “cruzamento tipo cruz”
- Vá para a esquerda ou
- Vá para a direita ou
- Siga em frente ou
- Em um “T”:
- Vá para a esquerda ou
- Vá para a direita
- Em um “virar somente a direita”:
- Vá para a direita
- Em um “virar somente a esquerda”:
- Vá para a esquerda
- Em um a frente ou esquerda:
- Vá para a esquerda ou
- Siga em frente
- Em um a frente ou ou a direita:
- Vá para a direita ou
- Siga em frente
- Em um beco sem saída:
- Volte
- No final do labirinto:
- Pare
Aplicando-se a “regra da mão esquerda” a lista acima, será reduzida a apenas uma opção para uma cada uma das possibilidades:
- Em um “cruzamento tipo cruz”
- Vá para a esquerda
- Em um “T” (Transversal):
- Vá para a esquerda
- Em um “virar somente a direita”:
- Vá para a direita
- Em um “virar somente a esquerda”:
- Vá para a esquerda
- Em um a frente ou esquerda:
- Vá para a esquerda
- Em um a frente ou ou a direita:
- Siga em frente
- Em um beco sem saída:
- Volte
- No final do labirinto:
- Pare
Estamos quase lá. Quando o robô atinge um beco sem saída é fácil identificá-lo, porque não existem situações ambíguas (já implementamos essa ação com o Robô seguidor de linha). O problema está quando o robô encontra uma “linha” por exemplo, pois a linha pode ser parte de um cruzamento tipo “cruz” (1) ou de um “T” (2) ou mesmo um “Final” (8). Além disso, quando o robô chega a um “virar à esquerda ou à direita”, esses cruzamentos podem ser os do tipo simples (opções 3 ou 4) ou opções que podem ir para a frente (5 ou 6). Para se descobrir exatamente em que tipo de intersecção está o robô, é necessário incorporar um passo adicional: o robô deve “dar um passinho a frente” ou seja rodar o que chamamos de “extra inch” e assim “ver” o que vem por adiante:
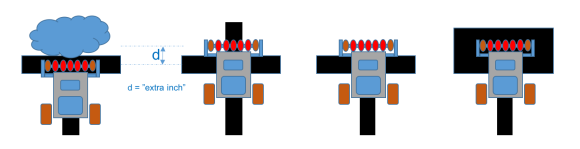
Em termos de fluxo, todas as acções possíveis podem ser descritas como:
- Em um beco sem saída:
- Volte
- Em uma linha:
- Executar uma polegada extra
- Se há uma linha:
- É uma “cruz” ==> Ir para ESQUERDA
- Se não houver nenhuma linha:
- é um “T” ==> Ir para ESQUERDA
- Se houver outra linha:
- É o fim de Maze ==> PARAR
- Em uma curva à direita:
- Executar uma polegada extra
- se há uma linha:
- É ir a frente ou virar a direita ==> ir direto
- Se não houver nenhuma linha:
- é um virar obrigatoriamente a direita==> Ir para DIREITA
- Em uma curva à esquerda:
- Executar uma polegada extra
- se há uma linha:
- É ir a frente ou virar a esquerda ==> virar a esquerda
- Se não houver nenhuma linha:
- é um virar obrigatoriamente a esquerda==> Ir para ESQUERDA
Note-se que de facto, no caso de um “virar à esquerda”, você poderá pular o teste porque o robô tomará à esquerda de qualquer maneira. Deixei a explicação mais genérica somente para claridade. No código real ignorarei este teste.

A foto ao lado , é de um labirinto bem simples que desenhei no chão do meu laboratório, usando fita isolante de 18mm (3/4) que uso para testes (ainda bem que minha mãe não viu!!!! ;-0:
Aplicando o algorítmo “Left Hand on the Wall” ao código do Arduino
Uma vez que já temos a função readLFSsensors () modificada, para incluir os 2 sensores adicionais, podemos também re-escrever a função “Loop” introduzindo o algoritmo como descrito anteriormente:
void loop()
{
readLFSsensors();
switch (mode)
{
case NO_LINE:
motorStop();
goAndTurn (LEFT, 180);
break;
case CONT_LINE:
runExtraInch();
readLFSsensors();
if (mode == CONT_LINE) mazeEnd();
else goAndTurn (LEFT, 90);
break;
case RIGHT_TURN:
runExtraInch();
readLFSsensors();
if (mode == NO_LINE) goAndTurn (RIGHT, 90);
break;
case LEFT_TURN:
goAndTurn (LEFT, 90);
break;
case FOLLOWING_LINE:
followingLine();
break;
}
}
Algumas funções importantes aparecem aqui.
followingLine() é a mesma utilizada com o robô seguidor de linha, que quando se está apenas seguindo uma linha, deve-se: calcular o PID e controlar os motores, dependendo dos valores dos ganhos da malha de controle usando a função: motorPIDcontrol ();
runExtraInch (): vai empurrar o robô para a frente um pouquinho. Quanto o robô se moverá, dependerá do tempo que você usa na função delay(), antes que mande parar os motores.
void runExtraInch(void)
{
motorPIDcontrol();
delay(extraInch);
motorStop();
}
goAndTurn (direction, angle): Esta função é importante, porque você na verdade não pode virar o robô, tão logo perceba o tipo de intersecção em que está. Lembre-se que projectamos um robô do tipo diferencial que, quando faz curvas, “gira em torno do seu eixo”. Assim, para sair de um cruzamento, girar 90 graus e continuar movendo-se sobre a linha, o centro das rodas deve obrigatoriamente estar alinhado com o centro da intersecção. Uma vez que a linha dos sensores está à frente do eixo das rodas, o robô deve mover-se para a frente para alinhá-los. Os moteres devem funcionar por um tempo “t” dependendo da distância entre a linha dos sensores e o eixo dos motores ( “d”), velocidade e tamanho das rodas. Esta constante de tempo “t” é no código: adjGoAndTurn, que deve ser ajustada dependendo de seu projeto:

void goAndTurn(int direction, int degrees)
{
motorPIDcontrol();
delay(adjGoAndTurn);
motorTurn(direction, degrees);
}
Neste ponto, o robô já está “resolvendo um labirinto”! Você acabou de terminar o “Primeiro Passo”. Não importa onde você começar dentro de um labirinto, você chegará ao final.
Abaixo, um vídeo mostrando um teste para esta fase do projeto:
Tomando nota do Caminho
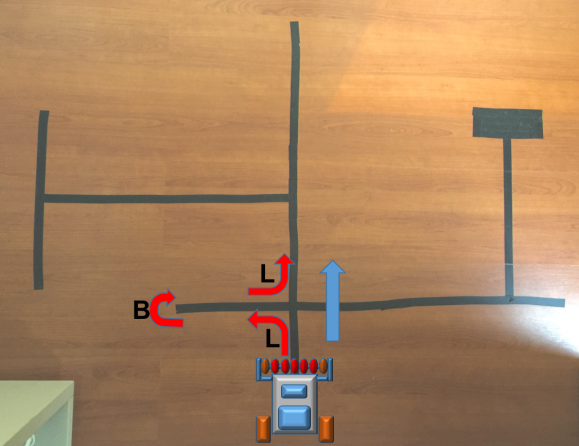
Consideremos o exemplo abaixo:

Partindo do ponto escolhido, o robô encontrará 15 Interseções antes de chegar ao final do labirinto:
- Esquerda (L)
- Back (B)
- Esquerda (L)
- Esquerda (L)
- Esquerda (L)
- Back (B)
- Reto (S)
- Back (B)
- Esquerda (L)
- Esquerda (L)
- Back (B)
- Reto (S)
- Esquerda (L)
- Esquerda (L)
- Fim
O que deve ser feito em qualquer um desses cruzamentos é “salvar a decisão tomada” na mesma sequência em que aconteça. Para isso, vamos criar uma nova variável (matriz) que irá armazenar o caminho que o robô tenha tomado:
A variável path[] e 2 índices variáveis, serão utilizados em conjunto para se gravar os passos:
char path[100] = ""; unsigned char pathLength = 0; // the length of the path int pathIndex = 0; // used to reach an specific array element.
Voltando ao exemplo, uma vez percorrido todo o circuito, as variáveis ficariam:
path = [LBLLLBSBLLBSLL] e pathLengh = 14
Simplificando (otimizando) o Caminho
Voltemos ao nosso exemplo. Olhando para o primeiro grupo de cruzamentos, percebemos que o primeiro ramo esquerdo é na verdade um “Dead End”, e assim, se o robô em vez de um “lateral-esquerdo-esquerdo” apenas tivesse seguido reto nesse primeiro cruzamento, uma grande quantidade de energia e tempo seriam salvas! Em outras palavras, uma sequência do tipo “LBL”, de facto, seria o mesmo que “S”.
Isso é exatamente como o caminho completo pode ser otimizado. Se você analisar todas as possibilidades onde um “U turn” (back) é utilizado, o conjunto de 3 cruzamentos onde o”U-Turn” ( “B”) aparece (“xBx”) poderá ser reduzido para apenas um.
A descrição acima é apenas um exemplo, abaixo podemos encontrar a lista completa de possibilidades:
LBR = B
LBS = R
RBL = B
SBL R =
SBS = B
LBL = S
Aplicando-se as substituições acima para o caminho completo de nosso exemplo, podemos reduzi-lo a:
path = [LBLLLBSBLLBSLL] ==> LBL = S
path = [SLLBSBLLBSLL] ==> LBS = R
path = [SLRBLLBSLL] ==> RBL = B
path = [SLBLBSLL] ==> LBL = S
path = [SSBSLL] ==> SBS = B
path = [SBLL] ==> SBL = R
path = [RL]
Olhando para o exemplo, é muito claro que se o robô gira para a DIREITA logo no primeiro cruzamento e depois disso, à esquerda, ele chegará ao final do labirinto pelo caminho mais curto!

A primeira passada será consolidada na função mazeSolve (). Esta função é, de facto, a função loop () utilizada anteriormente, onde se incorporaram as etapas de armazenamento e otimização do caminho. Quando a primeira passada termina, a variavel path[] conterá o caminho já optimizado.
Uma nova variável é introduzida para sinalizar o final da “passada”:
unsigned int status = 0; // solving = 0; reach end = 1
Abaixo a função completa para a primeira etapa do programa:
void mazeSolve(void)
{
while (!status)
{
readLFSsensors();
switch (mode)
{
case NO_LINE:
motorStop();
goAndTurn (LEFT, 180);
recIntersection('B');
break;
case CONT_LINE:
runExtraInch();
readLFSsensors();
if (mode != CONT_LINE) {goAndTurn (LEFT, 90); recIntersection('L');} // or it is a "T" or "Cross"). In both cases, goes to LEFT
else mazeEnd();
break;
case RIGHT_TURN:
runExtraInch();
readLFSsensors();
if (mode == NO_LINE) {goAndTurn (RIGHT, 90); recIntersection('R');}
else recIntersection('S');
break;
case LEFT_TURN:
goAndTurn (LEFT, 90);
recIntersection('L');
break;
case FOLLOWING_LINE:
followingLine();
break;
}
}
}
Aqui uma nova função foi introduzida: recIntersection (direction)
Esta função será a usada para armazenar as decisões tomadas nos cruzamentos e também para chamar outra importante função: simplifyPath(), que irá otimizando “em tempo real” o grupo de 3 cruzamentos envolvendo “U-Turn”, como vimos anteriormente.
void recIntersection(char direction)
{
path[pathLength] = direction; // Store the intersection in the path variable.
pathLength ++;
simplifyPath(); // Simplify the learned path.
}
O crédito para a criação da função simplifyPath () é de Patrick McCabe. Eu apenas a incluí ao meu código (para mais detalhes, visite patrickmccabemakes.com):
void simplifyPath()
{
if(pathLength < 3 || path[pathLength-2] != 'B') // only simplify the path if the second-to-last turn was a 'B'
return;
int totalAngle = 0;
int i;
for(i=1;i<=3;i++)
{
switch(path[pathLength-i])
{
case 'R':
totalAngle += 90;
break;
case 'L':
totalAngle += 270;
break;
case 'B':
totalAngle += 180;
break;
}
}
totalAngle = totalAngle % 360; // Get the angle as a number between 0 and 360 degrees.
switch(totalAngle) // Replace all of those turns with a single one.
{
case 0:
path[pathLength - 3] = 'S';
break;
case 90:
path[pathLength - 3] = 'R';
break;
case 180:
path[pathLength - 3] = 'B';
break;
case 270:
path[pathLength - 3] = 'L';
break;
}
pathLength -= 2; // The path is now two steps shorter.
}
A segunda passada: resolvendo o labirinto o mais rápido possível!
O programa principal: loop () é bem simples:
void loop()
{
ledBlink(1);
readLFSsensors();
mazeSolve(); // First pass to solve the maze
ledBlink(2); // end 1st pass
while (digitalRead(buttonPin) && !mode) { }
pathIndex = 0;
status = 0;
mazeOptimization(); //run the maze as fast as possible
ledBlink(3); // end of 2nd pass. Maze solved!
}
Assim, quando a primeira passada termina, o que devemos fazer é apenas “alimentar” o robô com o caminho otimizado. Ele vai começar a percorrer o labirinto novamente e quando uma intersecção for encontrado, ele não mais tomará decisões, mas simplesmente seguirá o que está armazenado na variável path [].
Para a segunda passada usamos a função mazeOptimization(), que por sua vez, chama a função mazeTurn(path[]) que comandará os movimentos do robô nessa segunda passada:
void mazeOptimization (void)
{
while (!status)
{
readLFSsensors();
switch (mode)
{
case FOLLOWING_LINE:
followingLine();
break;
case CONT_LINE:
if (pathIndex >= pathLength) mazeEnd ();
else {mazeTurn (path[pathIndex]); pathIndex++;}
break;
case LEFT_TURN:
if (pathIndex >= pathLength) mazeEnd ();
else {mazeTurn (path[pathIndex]); pathIndex++;}
break;
case RIGHT_TURN:
if (pathIndex >= pathLength) mazeEnd ();
else {mazeTurn (path[pathIndex]); pathIndex++;}
break;
}
}
}
void mazeTurn (char dir)
{
switch(dir)
{
case 'L': // Turn Left
goAndTurn (LEFT, 90);
break;
case 'R': // Turn Right
goAndTurn (RIGHT, 90);
break;
case 'B': // Turn Back
goAndTurn (RIGHT, 180);
break;
case 'S': // Go Straight
runExtraInch();
break;
}
}
A segunda passada está feita!
O vídeo abaixo mostra o exemplo trabalhado aqui completo, onde Rex encontra seu caminho para livrar-se do Minotauro! 😉
O código Arduino completo para este projeto, poderá ser encontrado no link abaixo:
Usando o aplicativo Android para o ajuste
A App Android desenvolvido para o projeto do Robô seguidor de Linha também pode ser usado aqui. O código Arduino apresentado na última etapa já inclui comunicação com o dispositivo Android, mas se não quiser usar-lo não há problema, porque o código é “transparente”.
Eu usei bastante o dispositivo Android durante o projeto para enviar dados de teste do robô para o dispositivo, utilizando-se o campo de “Mensagem recebida”.
Diversas variáveis devem ser bem definidas, a fim de garantir que o robô gire corretamente. Os mais importantes estão abaixo (os marcados em negrito tive mudar-los várias vezes):
const int power = 250; const int iniMotorPower = 250; const int adj = 0; float adjTurn = 8; int extraInch = 200; int adjGoAndTurn = 800; const int THRESHOLD = 150; float Kp=50; float Ki=0; float Kd=0;
CONCLUSÃO
Esta é a segunda e última parte de um projeto complexo, explorando a potencialidade de um robô seguidor de linha, onde aplicando-se conceitos de inteligência artificial se conseguiu explorar labirintos, encontrando o caminho da saída mais curto e rápido.
Espero que esse trabalho possa contribuir para que outras pessoas possam aprender mais sobre eletrônica, robôs, Arduino, etc.
Não deixe de visitar e seguir minha página: MJRoBot.org no Facebook
Saludos desde el sur del mundo! 😉
Um abraço e até o próximo post!
Obrigado
Marcelo













Olá marcelo, poderia tirar uma duvida por favor, já olhei o artigo anterior e mesmo assim não estou tendo sucesso. bom estou usando 2 servos as3103pg, unicos que eu encontrei sendo 360, e não consigo para-los, ligo o arduino e eles continuam rodando sem parar, já setei para 1500microseconds, pra 2000, pra varios valores e parece que eles não compreendem, esses valores eu mudo no motorFunctions, certo?! só está faltando isso pro projeto sair e assim que funcionar eu mando fotos\videos pra você ver 😀 valeu
CurtirCurtir
Boa noite Marcelo, estou com 3 duvidas.
A primeira é em relação ao corpo do veiculo, as rodas com os motores na frente e a roda boba/solta atrás isso num vai influenciar em muita coisa, certo?!
A segunda é em relação ao button instalado, eu fiz exatamente igual ao projeto e mesmo assim o robô já liga querendo andar, não aperto o botão e ele já sai tentando achar um caminho, será que tem algo errado? Eu nunca entendi muito bem o lado que liga o gnd e a outra parte até porque os lados são iguais do button hahahaha.
E a outra duvida em com os sensores tcrt5000, quando eu coloco o carrinho no chão e ele já sai andando, parece que a sombra dos sensores atrapalha pra detectar o caminho, a algo que eu possa fazer? talvez subir os sensores, não sei bem.
De resto muito obrigado, ficou bem legal o projeto 😀
CurtirCurtir
Em princípio a rodinha na faz diferença, mas o melhor é ter a “tração na dianteira”, com a “rodinha boba”, como ”seguidora” das fracionadas.
Com relação ao botão, você deve ter se confundido com a lógica. Eu não me lembro do projeto (estou respondendo do celular), mas em geral gosto de usar um resistor de pull-up interno, o que faz com que o pino esteja sempre em “1” e ao pressionar o botão, vai a “0”. Assim seu código tem que levar em consideração que o pino sem ativação estará em “High” e só quando ativo vai a “Low”.
CurtirCurtir
Olá Marcelo.
Eu não tenho sensores refletivos infravermelho ANALÓGICOS, só Digitais, pode fazer com somente com digital?
CurtirCurtir
Encontrei uma possível solução……
Aquele sensor tcrt5000 (sem a Shield, somente o tsrt5000) funciona também .
CurtirCurtir
Oi Paulo. Na verdade o projeto funciona com sinais digitais mesmo (tem luz, não tem luz). É que como não tinha todos iguais, tive que usar alguns que só forneciam sinais análogicos e outros já digitais. Mas observe que em geral, mesmo os sensores que fornecem “uma saída digital”, o que fazem é leitura de um nível de luz. Usualmente existe uma pequeno potenciometro na placa para voce regular o que considera ser “preto”/”branco”.
CurtirCurtir
Ótimo material, bem detalhado e muito bem explicado! Parabéns! Obrigado por compartilhar um material de qualidade, continue assim
CurtirCurtir
Valeu Arthur. Muito obrigado. 😉
CurtirCurtir